2.3.3 Valores en los puntos de integración

El análisis de cualquier problema geotécnico debe contemplar el control de las tensiones efectivas, presiones de poros, deformaciones permanentes, etc. Estos valores son calculados a nivel de los puntos de integración de los elementos del modelo durante integración del modelo de comportamiento. En algunas ocasiones, también es importante observar las variables internas del modelo para comprender el comportamiento observado a nivel esfuerzos. Esta etapa es muy importante si se está desarrollando un modelo o si se desea evaluar la capacidad de un modelo para reproducir un determinado fenómeno.

La información a nivel de los elementos también se encuentra almacenada en el archivo binario *_SAVE pero su lectura es un poco más compleja. Para simplificar el análisis es posible emplear desde Matlab la función:

>> [POS,HIST]=gef_hist_intpoints(data);

la función básicamente recupera de un problema la ubicación y valores en los puntos de integración. La estructura data permite definir los valores a extraer:

data =
	    filename
        win
        var
        pos
        group

el campo filename debe especificar el nombre del archivo sin extensión, win define una ventana (rectangular en el caso 2D) para buscar los puntos de integración, var indica la posición de las variables de historia a extraer (dependen del modelo), pos permite seleccionar la posición inicial de los puntos de integración y group define los números de los grupos de elementos a considerar (ver help gef_hist_intpoints para mayores detalles).

A modo de ejemplo estudiaremos los resultados en el punto de integración en el extremo superior derecho (cerca del nodo 4). Para ello emplearemos los valores siguientes:

>> data.filename='BXDMC1';
>> data.win=[.5 1. .5 1.];
>> data.var=1:8;
>> data.pos=0;
>> data.group=1;
>> [POS,HIST]=gef_hist_intpoints(data);

con el nombre de archivo correspondiente y la ventana definida de forma de considerar sólo el punto de integración deseado (formato [ymin ymax zmin zmax]). En todos los modelos 2D en deformaciones planas, las variables 1 a 4 corresponden a los esfuerzos efectivos $\sigma_{yy}'$, $\sigma_{zz}'$, $\sigma_{yz}$ y $\sigma_{xx}'$; y las 5 a 8 a las 4 deformaciones $\varepsilon_{yy}$, $\varepsilon_{zz}$, $\gamma_{yz}$ y $\varepsilon_{xx}$ (notar que se trata de las distorsiones y no las deformaciones angulares). El valor data.pos=0 indica que sólo se calculará la posición inicial de los puntos de integración:

>> POS

POS =

    0.7887    0.7887

Como se trabaja en pequeñas deformaciones, todos los cálculos se efectúan en la configuración de referencia de forma que en términos estrictos calcular el desplazamiento de los puntos de integración. Sin embargo, para la visualización de algunos aspectos especiales de algunos modelos de comportamiento (fisuración difusa, deslizamiento en planos orientados, etc) conviene emplear esta información para fines únicamente gráficos. El campo data.group=1 indica que se estudiará el único grupo presente en el problema.

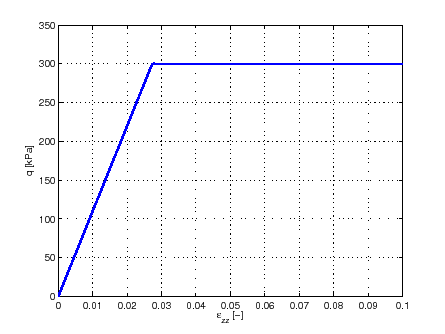
Similarmente a UNOD, HIST es una matriz de 3 índice, el primero corresponde al punto de integración (coincide con el primer índice de POS), el segundo corresponde a la variable pedida (1 a 8 en este caso) y el tercero al paso de análisis (240 en este ejemplo). Entonces, para trazar por ejemplo la variación del desviador $q=\sigma_{zz}'-\sigma_{yy}'$ en función de la deformación vertical $\varepsilon_{zz}$ se puede emplear el código:

Ezz=squeeze(HIST(1,6,:));
Q=squeeze(HIST(1,2,:))-squeeze(HIST(1,1,:));
figure
plot(Ezz,-1e-3*Q,'LineWidth',2)
xlabel('\epsilon_{zz} [-]')
ylabel('q [kPa]')
set(gca,'XDir','Reverse')
grid on

Con el cual se obtiene:

Como GEFDyn trabaja con la convención de la mecánica del continuo se multiplicaron los esfuerzos por $-1 \times 10^{-3}$ en la figura, aprovechando de cambiar las unidades a [kPa]. Las deformaciones normales se multiplicaron por $-1$.

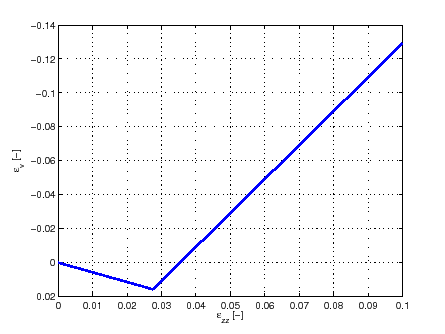
Similarmente se puede obtener la variación de volumen $\varepsilon_v$ de la muestra en función de la deformación vertical $\varepsilon_{zz}$:

Eyy=squeeze(HIST(1,5,:));
figure
plot(Ezz,Ezz+Eyy,'LineWidth',2)
xlabel('\epsilon_{zz} [-]')
ylabel('\epsilon_v [-]')
set(gca,'XDir','Reverse')
grid on

que pone de manifiesto claramente el cambio de comportamiento contractivo a dilatante.