3.3.3 Cálculo dinámico inelástico

El archivo para efectuar el cálculo dinámico inelástico es exactamente el mis que el elástico, cambiando sólo el valor de la amplitud del campo incidente AMPLS=1.0 para no escalar el movimiento.

Para poner de manifiesto el comportamiento no lineal, podemos observar por ejemplo las deformaciones volumétricas plásticas $\varepsilon_v^p$ en el suelo (negativas indican contracción):

> gef_video('col_dyn_2d_nl',1,'evp')
> fecom('scalecoef 20')

por lo tanto la máxima deformación volumétrica plástica ocurre cerca del centro del estrato arenoso.

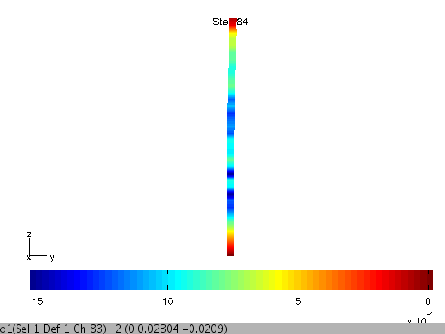
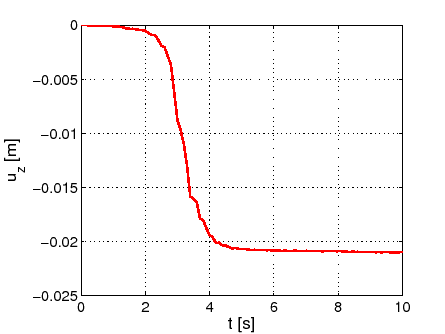
Para poner de manifiesto el comportamiento inelástico del suelo, podemos observar el asentamiento calculado en superficie:

> %Settlement
> file_gef='col_dyn_2d_nl';
> MODEL=gefread([file_gef,'.in']);
> NodeID=feutil('findnode y==0. & z==0.',MODEL);
> UNOD=gefread([file_gef,'_SAVE UNOD']);
> TIME=gefread([file_gef,'_SAVE TIME']);
> 
> figure
> plot(TIME,squeeze(UNOD(NodeID,3,:)),'-r')
> grid on
> xlabel('t [s]')
> ylabel('u_z [m]')
> format_figures

por lo tanto se obtiene un asentamiento co-sísmico de un poco más de 2 [cm].

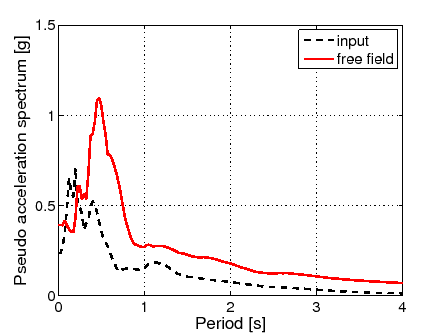
Finalmente, conviene por ejemplo chequear el espectro de respuesta (pseudo aceleraciones) en superficie en comparación al correspondiente al input:

> %Spectra
> %input (outcrop)
> CURVES=stack_get(MODEL,'curve'); CASE=stack_get(MODEL,'case');
> if CURVES{3}.type(2)==2; Time=linspace(CURVES{3}.data(1),...
>                CURVES{3}.data(2)*CURVES{3}.type(3),CURVES{3}.type(3)); end
> Input=1*CURVES{3}.data(3:end);
> udd.Deltat = mean(diff(Time));
> udd.Value = Input;
> [T,Sd,PSV,PSA_input] = Elastic_Response_Spectrum(udd,[0 5],200,0.05);
> %free field (computed)
> ANOD=gefread([file_gef,'_SAVE ANOD']);
> udd.Deltat = mean(diff(TIME));
> udd.Value = squeeze(ANOD(NodeID,2,:));
> [T,Sd,PSV,PSA_ff] = Elastic_Response_Spectrum(udd,[0 5],200,0.05);
>
> figure
> plot(T,PSA_input/9.81,'--k',T,PSA_ff/9.81,'-r')
> grid on
> xlim([0 4])
> ylabel('Pseudo acceleration spectrum [g]')
> xlabel('Period [s]')
> legend('input','free field')
> format_figures

En los espectros anteriores se observa perfectamente tanto al aumento de amplitudes debido al efecto de sitio, así como la variación del contenido de frecuencias del movimiento en campo libre en relación al registrado en el afloramiento rocoso empleado como ``input'' para el modelo.