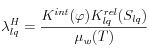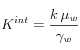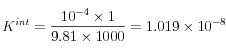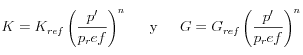El presente tutorial ilustra la resolución de un problema de consolidación 1D bifásico (hidro-mecánico), completamente acoplado.
Se estudian tres escenarios de modelación:
Geometría
Consideraremos un estrato uniforme, completamente saturado y apoyado sobre una roca impermeable. La altura del estrato es igual a 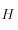 :
:
Los parámetros que caracterizan el problema son:
||Parámetros del problema|Table Summary||
| {{Constante}} | {{Valor}} | {{Unidades}} |
|  |
| 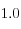 | MPa |
|
| MPa |
| 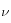 |
| 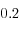 | - |
|
| - |
| 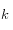 |
| 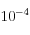 | m/s |
|
| m/s |
| 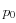 |
| 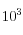 | Pa/m |
|
| Pa/m |
| 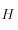 |
| 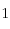 | m |
|
| m |
| 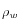 |
| 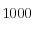 | kg/m3 |
|
| kg/m3 |
| 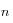 |
|  | - |
|
| - |
| 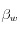 |
| 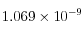 | 1/Pa |
|
| 1/Pa |
|  |
| 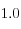 | Pa s |
| Pa s |
donde  es el módulo de Young del suelo,
es el módulo de Young del suelo, 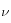 su módulo de Poisson y
su módulo de Poisson y 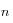 su porosidad. La permeabilidad del suelo al agua es
su porosidad. La permeabilidad del suelo al agua es 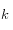 y la carga aplicada es
y la carga aplicada es 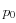 [[este valor es irrelevante para el caso elástico, pero es importante para el caso inelástico ya que afecta el nivel de deformaciones plásticas desarrolladas en el suelo]]. El agua está caracterizada por su densidad de masa
[[este valor es irrelevante para el caso elástico, pero es importante para el caso inelástico ya que afecta el nivel de deformaciones plásticas desarrolladas en el suelo]]. El agua está caracterizada por su densidad de masa 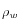 , el inverso de su compresibilidad
, el inverso de su compresibilidad 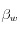 y su viscosidad dinámica
y su viscosidad dinámica 
Solución analítica
El problema de consolidación unidimensional puede ser resuelto analíticamente por medio de la ecuación diferencial parcial:
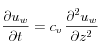
donde
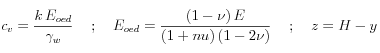
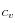 es el coeficiente de consolidación, mientras que
es el coeficiente de consolidación, mientras que 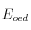 es el módulo de compresión edométrico (módulo de Young con deformación lateral restringida). La solución analítica de la ecuación diferencial parcial, asumiendo comportamiento elástico, se puede escribir en términos de la serie:
es el módulo de compresión edométrico (módulo de Young con deformación lateral restringida). La solución analítica de la ecuación diferencial parcial, asumiendo comportamiento elástico, se puede escribir en términos de la serie:
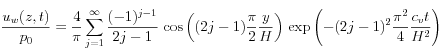
La expresión anterior permite cuantificar la disipación de la sobre presión de poros 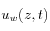 con respecto a la carga total impuesta
con respecto a la carga total impuesta 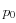 a una profundidad
a una profundidad 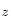 y un tiempo
y un tiempo 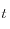 . La expresión anterior no considera gravedad, por lo tanto la presión de poros como los esfuerzos efectivos son inicialmente nulos.
. La expresión anterior no considera gravedad, por lo tanto la presión de poros como los esfuerzos efectivos son inicialmente nulos.
Conductividad hidráulica
En Code_Aster lo modelación hidro-mecánica acoplada THHM [1] emplea una ecuación de difusión de la fase fluida de la forma:

donde
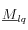
es el flujo másico del líquido y
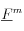
son las fuerzas de masa (gravedad). El flujo másico se puede relacionar a la velocidad de las fases líquida
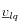
y sólida
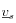
como:
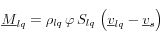
donde
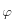
es la porosidad Euleriana (porosidad actual incluyendo deformaciones del esqueleto sólido) y
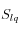
es el grado de saturación en líquido. La densidad de masa del líquido
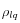
corresponde a la combinación de la densidad de masa del fluido
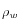
y la del gaz disuelto
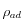
:
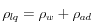
Bajo las hipótesis de {{pequeñas deformaciones}}, {{sin gaz disuelto}} y material {{saturado}} la ecuación de difusión líquida resulta:
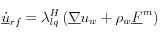
En mecánica de suelos, el flujo de un fluido a través de un suelo se caracteriza a través de la ecuación de Darcy. Si el suelo es isotrópico esta relación queda:
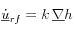
donde
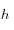
es la carga hidráulica:
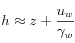
despreciando el término inercial debido a que los flujos se asumen razonablemente lentos. Luego, comparando la expresión de {Code_Aster} y la ley de Darcy, se obtiene que:
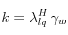
Por otro lado, el valor de
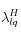
se calcula en {Code_Aster} como una función de la permeabilidad geométrica o intrínseca
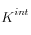
(función de la porosidad Euleriana
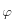
), la permeabilidad relativa del sólido al fluido
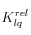
(depende de la sección disponible para el tránsito del fluido y por lo tanto de la saturación
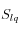
) y de la viscosidad del fluido

(a cierta temperatura):
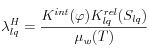
Si el suelo está saturado, podemos suponer que
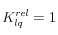
. Luego, el valor de la permeabilidad intrínseca
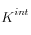
{{compatible}} con el valor "geotécnico"
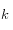
entregado es de:
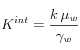
Evaluando en los datos disponibles se obtiene:
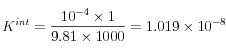
{{{Caso 1: Material elástico sin gravedad}}}
En este caso, ya que el esqueleto es elástico, no se requiere de una inicialización de la fase sólida. Como el problema no tiene gravedad, los resultados se pueden comparar directamente en términos del perfil de presión de poros
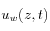
en varios instantes de tiempo
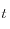
:
En este caso, como se trata de las mismas hipótesis empleadas para derivar la solución analítica, el ajuste de la solución numérica con el modelo de Elementos Finitos es excelente.
{{{Caso 2: Material elástico con gravedad}}}
Al incorporar la gravedad, tanto la fase sólida como la líquida adquieren peso. De esta forma, el estado inicial incluye presiones hidro-estáticas y tensiones verticales y horizontales geoestáticas. Para incorporar la gravedad, el cálculo se dividió en dos fases:
-* Se construye un modelo sin carga donde se inicializan las tensiones y las presiones debido a la gravedad. Ya que por peso propio el suelo tiende a asentarse, esta etapa toma un tiempo antes de que se estabilicen las tensiones y presiones (auto-consolidación). En el modelo se calculó entre 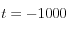 s y
s y 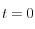 s
-* En la segunda fase del cálculo se incorpora la carga vertical (consolidación usual). De la primera fase se extrae el campo de tensiones y las presiones nodales. No se extraen los desplazamientos nodales con el objetivo de iniciar la segunda fase en términos relativos al equilibrio estático. Como las fuerzas de gravedad se equilibran con el campo de tensiones impuesto, no se producirán deformaciones por peso propio. Esta segunda fase comienza en
s
-* En la segunda fase del cálculo se incorpora la carga vertical (consolidación usual). De la primera fase se extrae el campo de tensiones y las presiones nodales. No se extraen los desplazamientos nodales con el objetivo de iniciar la segunda fase en términos relativos al equilibrio estático. Como las fuerzas de gravedad se equilibran con el campo de tensiones impuesto, no se producirán deformaciones por peso propio. Esta segunda fase comienza en 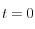 s y termina para
s y termina para 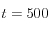 s.
Tal y como se esperaba, los resultados para el caso con o sin gravedad considerando el esqueleto sólido elástico son prácticamente idénticos. Desde el punto de vista téorico, las únicas diferencias están ligadas a la ecuación de difusión en la que aparace para el segundo caso la fuerza de gravedad. El resto de las hipótesis del problema se mantiene, lo que explica esta variación mínima con respecto a la solución teórica.
{{{Caso 3: Material inelástico con gavedad}}}
En este caso se empleó el modelo elasto-plástico multi-mecanismos de Hujeux. Para el caso inelástico se emplea exactamente la misma lógica del caso elástico con gravedad, es decir, se comienza con una inicialización de tensiones para luego seguir con la aplicación de la carga vertical y la consolidación.
El modelo de Hujeux incorpora nociones de elasticidad no lineal, de forma que los módulos elásticos de compresión
s.
Tal y como se esperaba, los resultados para el caso con o sin gravedad considerando el esqueleto sólido elástico son prácticamente idénticos. Desde el punto de vista téorico, las únicas diferencias están ligadas a la ecuación de difusión en la que aparace para el segundo caso la fuerza de gravedad. El resto de las hipótesis del problema se mantiene, lo que explica esta variación mínima con respecto a la solución teórica.
{{{Caso 3: Material inelástico con gavedad}}}
En este caso se empleó el modelo elasto-plástico multi-mecanismos de Hujeux. Para el caso inelástico se emplea exactamente la misma lógica del caso elástico con gravedad, es decir, se comienza con una inicialización de tensiones para luego seguir con la aplicación de la carga vertical y la consolidación.
El modelo de Hujeux incorpora nociones de elasticidad no lineal, de forma que los módulos elásticos de compresión  y el módulo de corte
y el módulo de corte 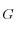 son funciones del confinamiento:
son funciones del confinamiento:
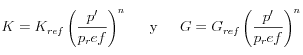
en función del confinamiento efectivo 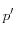 y de dos valores de referencia
y de dos valores de referencia 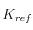 y
y 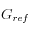 para un confinamiento de referencia
para un confinamiento de referencia 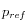 . Para desarrollar este ejemplo, se empleó
. Para desarrollar este ejemplo, se empleó 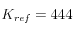 MPa y
MPa y 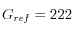 MPa, una presión de referencia
MPa, una presión de referencia 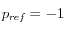 MPa y un coeficiente para la no linealidad de
MPa y un coeficiente para la no linealidad de 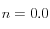 (módulos constantes)[[Para un problema real, los valores experimentales sugieren un valor de
(módulos constantes)[[Para un problema real, los valores experimentales sugieren un valor de 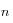 de alrededor de
de alrededor de 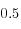 ]].
La comparación con la solución analítica elástica no es directa, ya que en el caso inelástico la compresibilidad del esqueleto sólido del suelo es muy superior. En efecto, las curvas teóricas elásticas de la figura (líneas segementadas) se evaluaron usando sólo el 1% de las rigideces elásticas
]].
La comparación con la solución analítica elástica no es directa, ya que en el caso inelástico la compresibilidad del esqueleto sólido del suelo es muy superior. En efecto, las curvas teóricas elásticas de la figura (líneas segementadas) se evaluaron usando sólo el 1% de las rigideces elásticas 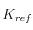 y
y 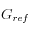 .
. Consolidación 1D
Consolidación 1D![]() :
: ![]() |
| ![]() | MPa |
|
| MPa |
| ![]() |
| ![]() | - |
|
| - |
| ![]() |
| ![]() | m/s |
|
| m/s |
| ![]() |
| ![]() | Pa/m |
|
| Pa/m |
| ![]() |
| ![]() | m |
|
| m |
| ![]() |
| ![]() | kg/m3 |
|
| kg/m3 |
| ![]() |
| ![]() | - |
|
| - |
| ![]() |
| ![]() | 1/Pa |
|
| 1/Pa |
| ![]() |
| ![]() | Pa s |
| Pa s |
![]() es el módulo de Young del suelo,
es el módulo de Young del suelo, ![]() su módulo de Poisson y
su módulo de Poisson y ![]() su porosidad. La permeabilidad del suelo al agua es
su porosidad. La permeabilidad del suelo al agua es ![]() y la carga aplicada es
y la carga aplicada es ![]() [[este valor es irrelevante para el caso elástico, pero es importante para el caso inelástico ya que afecta el nivel de deformaciones plásticas desarrolladas en el suelo]]. El agua está caracterizada por su densidad de masa
[[este valor es irrelevante para el caso elástico, pero es importante para el caso inelástico ya que afecta el nivel de deformaciones plásticas desarrolladas en el suelo]]. El agua está caracterizada por su densidad de masa ![]() , el inverso de su compresibilidad
, el inverso de su compresibilidad ![]() y su viscosidad dinámica
y su viscosidad dinámica ![]()
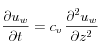
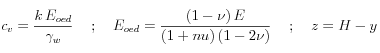
![]() es el coeficiente de consolidación, mientras que
es el coeficiente de consolidación, mientras que ![]() es el módulo de compresión edométrico (módulo de Young con deformación lateral restringida). La solución analítica de la ecuación diferencial parcial, asumiendo comportamiento elástico, se puede escribir en términos de la serie:
es el módulo de compresión edométrico (módulo de Young con deformación lateral restringida). La solución analítica de la ecuación diferencial parcial, asumiendo comportamiento elástico, se puede escribir en términos de la serie:
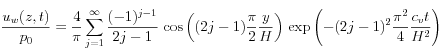
![]() con respecto a la carga total impuesta
con respecto a la carga total impuesta ![]() a una profundidad
a una profundidad ![]() y un tiempo
y un tiempo ![]() . La expresión anterior no considera gravedad, por lo tanto la presión de poros como los esfuerzos efectivos son inicialmente nulos.
. La expresión anterior no considera gravedad, por lo tanto la presión de poros como los esfuerzos efectivos son inicialmente nulos.

![]()
![]()
![]()
![]()
![]()
![]()